三相双绕组变压器

元件定义

该元件用以建模三相两绕组变压器（单线图，中性点内置）。

元件说明

属性

CloudPSS 元件包含统一的属性选项，其配置方法详见 参数卡 页面。

参数

Configuration

Configuration

参数名	键名	类型 [单位]	描述
Name	Name	文本	元件名称 此处输入三相双绕组变压器的名称（可缺省）
Rated Power	Tmva	实数 [MVA]	额定容量 变压器每侧绕组的额定容量$S_N$（所填变压器参数的功率基值）
Winding #1 Rated Voltage (L-L, RMS)	V1	实数 [kV]	绕组#1额定线电压有效值 绕组1的额定线电压有效值$V_{1N}$（所填变压器参数的电压基值）
Winding #2 Rated Voltage (L-L, RMS)	V2	实数 [kV]	绕组#2额定线电压有效值 绕组2的额定线电压有效值$V_{2N}$（所填变压器参数的电压基值）
Base Operation Frequency	f	实数 [Hz]	额定频率 变压器的额定频率$f_n$
Winding #1 Type	YD1	选择	绕组#1连接类型 选择绕组1的连接类型为星形(Y)或三角形(Delta)
Winding #2 Type	YD2	选择	绕组#2连接类型 选择绕组2的连接类型为星形(Y)或三角形(Delta)
Delta Lags or Leads Y	Lead	选择	Delta绕组连接方式 选择Delta连接绕组电压超前或滞后Y连接绕组电压30°，仅当有绕组为三角形连接时有效。
Winding #1 Neutral Point Resistance	Rn1	实数 [Ω]	绕组#1中性点电阻 绕组1的中性点接地电阻$r_{1n}$，仅在星形连接下有效
Winding #2 Neutral Point Resistance	Rn2	实数 [Ω]	绕组#2中性点电阻 绕组2的中性点接地电阻$r_{2n}$，仅在星形连接下有效
Positive Sequence Leakage Reactance	Xl	实数 [p.u.]	正序漏电抗 变压器的等值漏电抗$X_T$ ，可由变压器短路实验或变压器铭牌得出
Positive Sequence Leakage Resistance	Rl	实数 [p.u.]	正序漏电阻 变压器的等值漏电阻$R_T$ ，可由变压器短路实验或变压器铭牌得出
Magnetization Conductance	Gm	实数 [p.u.]	励磁电导 变压器励磁电导$G_M$，可由变压器空载实验或变压器铭牌得出
Magnetizing Current	Im1	实数 [%]	空载励磁电流 变压器器空载励磁电流$I_M$，可由变压器空载实验或变压器铭牌得出
Tap Changer	Tap	选择	变压器分接头选择 选择变压器分接头位置（无/绕组1/绕组2）
Initial Tap Ratio	InitTap	实数	初始分接头档位 填写变压器初始的分接头档位下的标幺值变比

Configuration-SFEMT

Configuration (For Shifted Frequency EMT)

参数名	键名	类型 [单位]	描述
Numerical Integration Method	NIM	选择	数值积分方法选择（仅对移频电磁暂态仿真有效）

Saturation

Saturation

参数名	键名	类型 [单位]	描述
Saturation Enabled	Enab	选择	考虑饱和特性? 选择“是”或“否”以开启或关闭铁芯饱和特性的建模
Place Saturation on	Sat	选择	励磁绕组位置 选择励磁绕组添加的位置，考虑饱和特性时，饱和电流由该位置注入
Air Core Reactance	Xac	实数 [p.u.]	空心电抗 变压器空心电抗，通常大约是等值漏电抗的两倍
Rush Decay Time Constant	Tdc	实数 [s]	涌流衰减时间 变压器励磁涌流的衰减时间常数
Knee Voltage	Xknee	实数 [p.u.]	拐点电压 对应于饱和曲线拐点的电压
Time to Release Flux Clipping	Txk	实数 [s]	启动时间 为防止启动不稳定，需要在一段时间内不计算或限制计算磁链值，该时间即为启动时间

Monitoring

Monitoring

参数名	键名	类型 [单位]	描述
Winding #1 Line Current Vector [kA]	I1	虚拟引脚（输出）	绕组1三相线电流 此处输入变压器绕组1三相线电流量测信号的标签（3×1维），如 I1ll
Winding #1 Phase Current Vector [kA]	I1p	虚拟引脚（输出）	绕组1三相相电流 此处输入变压器绕组1三相相电流量测信号的标签（3×1维），如 I1lg
Winding #2 Line Current Vector [kA]	I2	虚拟引脚（输出）	绕组2三相线电流 此处输入变压器绕组2三相线电流量测信号的标签（3×1维），如 I2ll
Winding #2 Phase Current Vector [kA]	I2p	虚拟引脚（输出）	绕组2三相相电流 此处输入变压器绕组2三相相电流量测信号的标签（3×1维），如 I2lg
Winding #1 RMS Line Current [kA]	I1rms	虚拟引脚（输出）	绕组1线电流均方根值 此处输入变压器绕组1电流有效值量测信号的标签（1×1维），如 I1rms
Winding #2 RMS Line Current [kA]	I2rms	虚拟引脚（输出）	绕组2线电流均方根值 此处输入变压器绕组2电流有效值量测信号的标签（1×1维），如 I2rms
Winding #1 Active Power [MW]	P1	虚拟引脚（输出）	绕组1有功功率 此处输入变压器绕组1有功功率量测信号的标签（1×1维），如 P1
Winding #1 Reactive Power [MVar]	Q1	虚拟引脚（输出）	绕组1无功功率 此处输入变压器绕组1无功功率量测信号的标签（1×1维），如 Q1
Winding #2 Active Power [MW]	P2	虚拟引脚（输出）	绕组2有功功率 此处输入变压器绕组2有功功率量测信号的标签（1×1维），如 P2
Winding #2 Reactive Power [MVar]	Q2	虚拟引脚（输出）	绕组2无功功率 此处输入变压器绕组2无功功率量测信号的标签（1×1维），如 Q2
3 Phase Magnetizing Current [kA]	Im	虚拟引脚（输出）	三相励磁电流 此处输入变压器励磁电流量测信号的标签（3×1维），如 Im
3 Phase Flux Linkage [KWb-N]	Flux	虚拟引脚（输出）	三相磁链 此处输入变压器磁链量测信号的标签（3×1维），如 Flux

引脚

引脚名	键名	类型	维度	描述
Pin #1	0	电气	3 × 1	变压器绕组1接线端
Pin #2	1	电气	3 × 1	变压器绕组2接线端
Tap	2	输入	1 × 1	变压器绕组1的分接头，输入变比控制信号
Tap	3	输入	1 × 1	变压器绕组2的分接头，输入变比控制信号
Primary Neutral Point	4	电气		一次侧中性点接线端（绕组1的连接类型为星形时有效）
Secondary Neutral Point	5	电气		二次侧中性点接线端（绕组2的连接类型为星形时有效）

模型说明

基础变压器模型

互感耦合模型
变压器最基本的数学模型来源于磁耦合绕组的互感关系。如下图所示，对于两个通过同一磁路耦合的绕组，其端口电压与电流之间的关系可由互感电感矩阵表示。

互耦合绕组

忽略铁耗与绕组电阻时，该关系可写为：

$$\begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \frac{d}{dt} \begin{bmatrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{bmatrix} \begin{bmatrix} i_1 \\ i_2 \end{bmatrix}$$

其中 $L_{11}$ 与 $L_{22}$ 分别为两个绕组的自感，$L_{12}=L_{21}$ 为绕组之间的互感。

为了在电磁暂态分析中由端口电压求解绕组电流，需要将上述关系改写为电流导数的形式，即对互感电感矩阵求逆：

$$\frac{d}{dt} \begin{bmatrix} i_1 \\ i_2 \end{bmatrix} = \mathbf{L}^{-1} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \tag{1}$$

互感电感矩阵的行列式为：

$$\Delta = L_{11} L_{22} - L_{12}^2 \tag{2}$$

通常引入耦合系数 $K$，定义为：

$$K = \frac{L_{12}}{\sqrt{L_{11} L_{22}}} \tag{3}$$

则行列式可写为：

$$\Delta = L_{11} L_{22} (1 - K^2) \tag{4}$$

由此可见，当两个绕组紧密耦合、共用磁路时，耦合系数 $K$ 接近于 1，互感矩阵的行列式趋近于零，其逆矩阵中的元素将迅速增大。这种情况下，互感矩阵呈现明显的数值病态特征，在数值求解中容易导致数值不稳定。

理想变压器模型
为避免互感矩阵求逆带来的数值问题，可将变压器建模为一种不显式包含励磁支路、仅由漏抗与匝比关系构成的理想变压器模型，如下图所示。

理想变压器

以两绕组理想变压器为例，设匝比为 $a$，并以绕组 1 为参考侧，将绕组之间的等效漏感定义为从绕组 1 端口测得的漏感 $L$（$L=L_1+a^2L_2$）。在这种建模形式下，绕组电流导数与端口电压之间可直接表示为：

$$\frac{d}{dt} \begin{bmatrix} i_1 \\ i_2 \end{bmatrix} = \frac{1}{L} \begin{bmatrix} 1 & -a \\ -a & a^2 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \tag{6}$$

式 (6) 可由短路试验等效电路推导得到：在一侧短路、另一侧施加电压的条件下，绕组电流变化完全由漏感决定，而理想变压器仅用于维持两侧电压与电流之间的比例关系。

基础变压器模型
在理想变压器模型的基础上进一步引入绕组损耗、铁芯损耗和铁芯饱和特性，从而形成基础变压器模型。如下图所示：

基础变压器模型

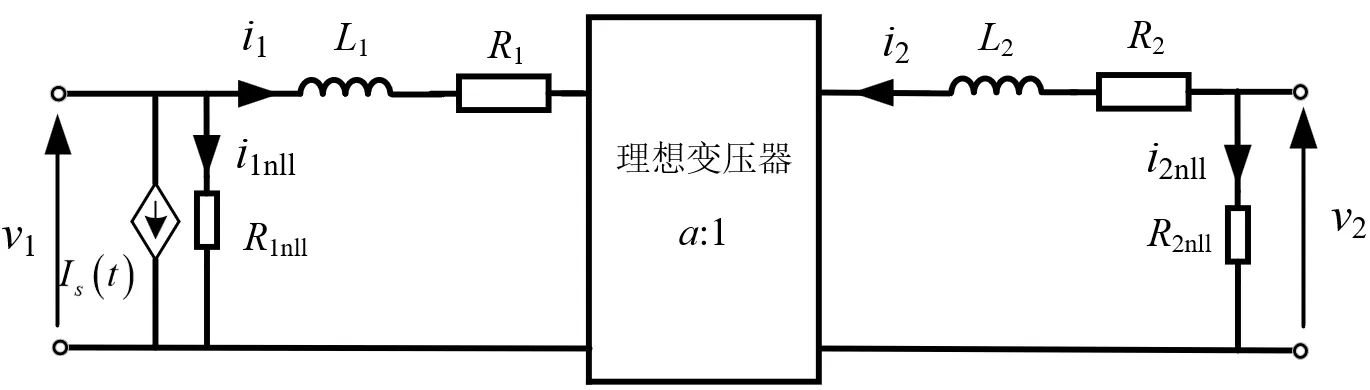
以两绕组变压器为例，$R_1$、$R_2$ 用于模拟铜损耗；$R_{1nll}$、$R_{2nll}$ 用于模拟空载损耗；$I_s(t)$为注入电流源，用于模拟变压器的饱和特性。

变压器饱和特性建模

变压器铁芯饱和源于铁磁材料磁化特性的非线性。当磁通处于较低水平时，铁芯磁化特性近似线性，所需的励磁电流较小；而当磁通逐渐接近材料的饱和值后，继续增加磁通将需要显著增大的励磁电流，铁芯由此进入饱和状态。

在电磁暂态仿真中，铁芯饱和可等效为一个非线性的励磁电感。实际模型中并不直接采用可变电感来表示这一非线性，而是通过在指定绕组端口并联一个注入电流源 $I_s(t)$ 来等效整个铁芯的磁化过程。该方法避免了由于电感值变化而在每个时间步重构系统矩阵的问题，从而具有良好的数值稳定性和计算效率。

饱和建模首先需要选定一个指定绕组，通常选为靠近铁芯的一侧绕组。设该绕组端口电压为 $V_1(t)$，铁芯的磁化磁链由该端口电压积分得到：

$$\lambda_S(t) = \int V_1(t)\,dt \tag{7}$$

注入电流源 $I_s$ 的电流由磁链 $\lambda_S$ 决定，其计算公式为：

$$I_s = \frac{\sqrt{(\lambda_S-\lambda_K)^2+4DL_A}+\lambda_S-\lambda_K}{2L_A} -\frac{D}{\lambda_K} \tag{8}$$

其中参数 $D$ 由下式确定：

$$D=\frac{-B-\sqrt{B^2-4AC}}{2A} \tag{9}$$

系数 $A$、$B$、$C$ 分别定义为：

$$A=\frac{L_A}{\lambda_K^2},\qquad B=\frac{L_A I_M-\lambda_M}{\lambda_K},\qquad C=I_M\,(L_A I_M-\lambda_M+\lambda_K) \tag{10}$$

上述参数中，$L_A$ 为空气磁路电感，用于描述铁芯在深度饱和区的渐近线性特性，通常取值为等值漏电感的两倍；$\lambda_M$ 为额定磁链，由额定电压和频率计算得到：

$$\lambda_M=\frac{V_M}{2\pi f} \tag{11}$$

拐点磁链 $\lambda_K$ 由拐点系数 $K$ （典型取值为1.15~1.25）与额定磁链确定，即：

$$\lambda_K = K\lambda_M$$

参数 $I_M$ 为额定磁链对应的励磁电流。通过上述参数，可以构造一条在低磁链区近似线性、在高磁链区逐渐过渡到空气磁路的非线性磁化特性。如下图所示：

磁化特性曲线

综上所述，由式 (8) 计算得到的励磁电流 $I_s$ 被直接注入到指定绕组端口，从而在电路层面等效铁芯在当前磁化状态下所需的励磁电流。随着磁链的变化，注入电流源能够自动反映铁芯由非饱和区向饱和区的过渡过程。

案例

常见问题